Single-Variable Distributions

This is a brief introduction to the functionality in prob140.

Getting Started

Make sure you are on the most recent version of the prob140 library. You can check your version of prob140 (or any other Python library) by running the following:

In [1]: import prob140

In [2]: print(prob140.__version__)
0.3.5.1

If you are using an iPython notebook, use this as your first cell:

# HIDDEN

from datascience import *
from prob140 import *
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('fivethirtyeight')

You may want to familiarize yourself with Data8’s datascience documentation first

Creating a Distribution

The prob140 library adds distribution methods to the default table class that you should already be familiar with. A distribution table is defined as a 2-column table in which the first column represents the possible values while the second column represents the probabilities associated with each value.

You can specify a list or array to the methods values and probability to specify those columns for a distribution

In [3]: from prob140 import *

In [4]: dist1 = Table().values(make_array(2, 3, 4)).probability(make_array(0.25, 0.5, 0.25))

In [5]: dist1
Out[5]: 
Value | Probability
2     | 0.25
3     | 0.5
4     | 0.25

We can also construct a distribution by explicitly assigning values for the values but applying a probability function to the values of the domain

In [6]: def p(x):
   ...:     return 0.25
   ...: 

In [7]: dist2 = Table().values(np.arange(1, 8, 2)).probability_function(p)

In [8]: dist2
Out[8]: 
Value | Probability
1     | 0.25
3     | 0.25
5     | 0.25
7     | 0.25

This can be very useful when we have a distribution with a known probability mass function

In [9]: from scipy.special import comb

In [10]: def pmf(x):
   ....:     n = 10
   ....:     p = 0.3
   ....:     return comb(n,x) * p**x * (1-p)**(n-x)
   ....: 

In [11]: binomial = Table().values(np.arange(11)).probability_function(pmf)

In [12]: binomial
Out[12]: 
Value | Probability
0     | 0.0282475
1     | 0.121061
2     | 0.233474
3     | 0.266828
4     | 0.200121
5     | 0.102919
6     | 0.0367569
7     | 0.00900169
8     | 0.0014467
9     | 0.000137781
... (1 rows omitted)

Events

Often, we are concerned with specific values in a distribution rather than all the values.

Calling event allows us to see a subset of the values in a distribution and the associated probabilities.

In [13]: dist1
Out[13]: 
Value | Probability
2     | 0.25
3     | 0.5
4     | 0.25

In [14]: dist1.event(np.arange(1,4))
Out[14]: 
Outcome | Probability
1       | 0
2       | 0.25
3       | 0.5

In [15]: dist2
Out[15]: 
Value | Probability
1     | 0.25
3     | 0.25
5     | 0.25
7     | 0.25

In [16]: dist2.event([1, 3, 3.5, 6])
Out[16]: 
Outcome | Probability
1       | 0.25
3       | 0.25
3.5     | 0
6       | 0

To find the probability of an event, we can call prob_event, which sums up the probabilities of each of the values.

In [17]: dist1.prob_event(np.arange(1,4))
Out[17]: 0.75

In [18]: dist2.prob_event([1, 3, 3.5, 6])
Out[18]: 0.5

In [19]: binomial.prob_event(np.arange(5))
Out[19]: 0.8497316673999995

In [20]: binomial.prob_event(np.arange(11))
Out[20]: 0.9999999999999992

Note that due to the way Python handles floats, there might be some rounding errors.

Plotting

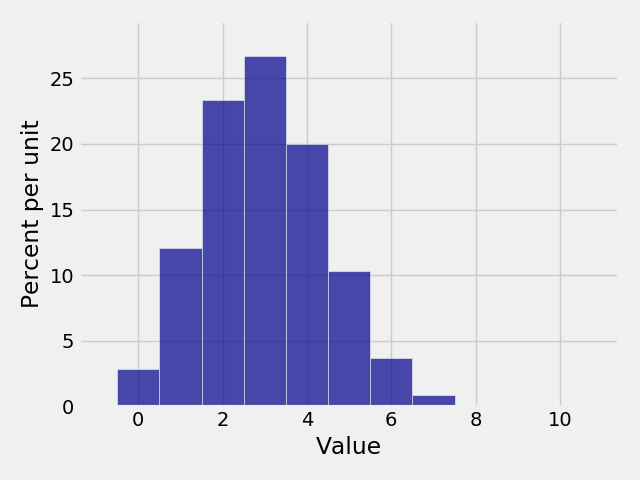
To visualize our distributions, we can plot a histogram of the probability mass function using the Plot function.

In [21]: Plot(binomial)

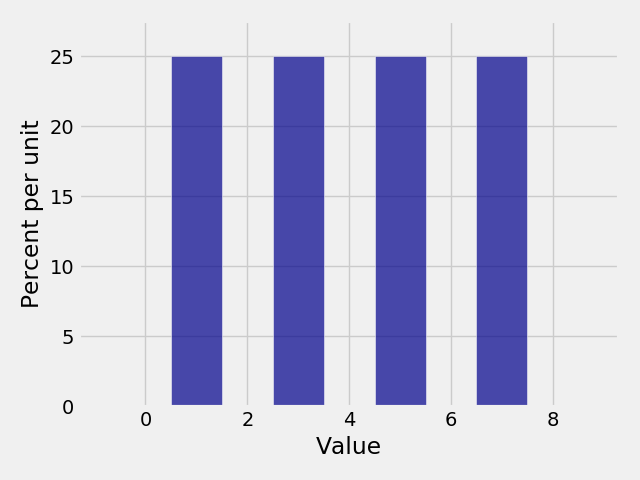
In [22]: Plot(dist2)

Width

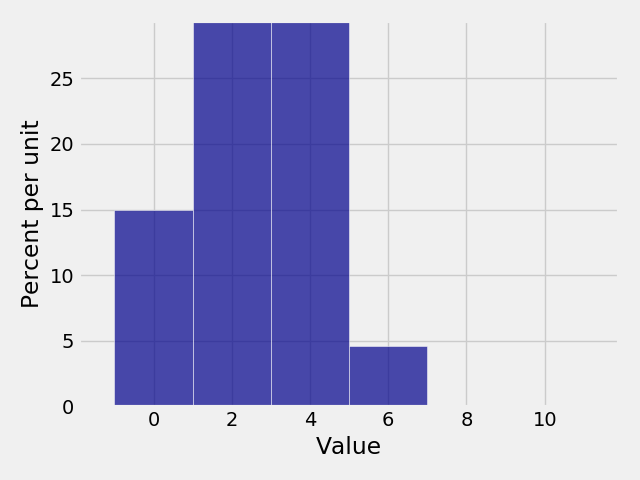
If want to specify the width of every bar, we can use the optional parameter width= to specify the bin sizes. However, this should be used very rarely, only when there is uniform spacing between bars.

In [23]: Plot(binomial, width=2)

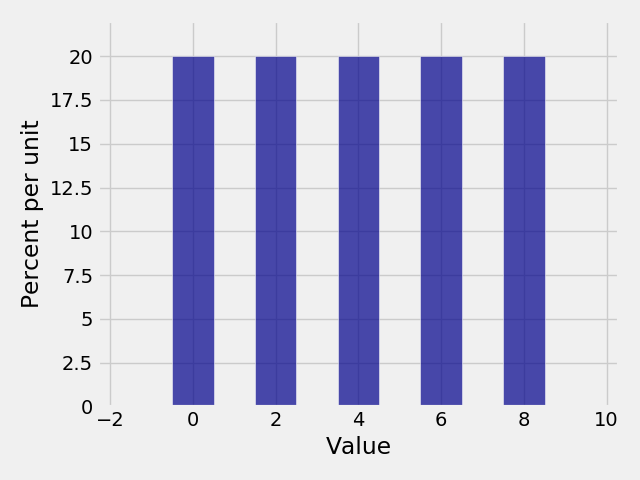
In [24]: dist3 = Table().values(np.arange(0, 10, 2)).probability_function(lambda x: 0.2)

In [25]: Plot(dist3)

In [26]: Plot(dist3, width=2)

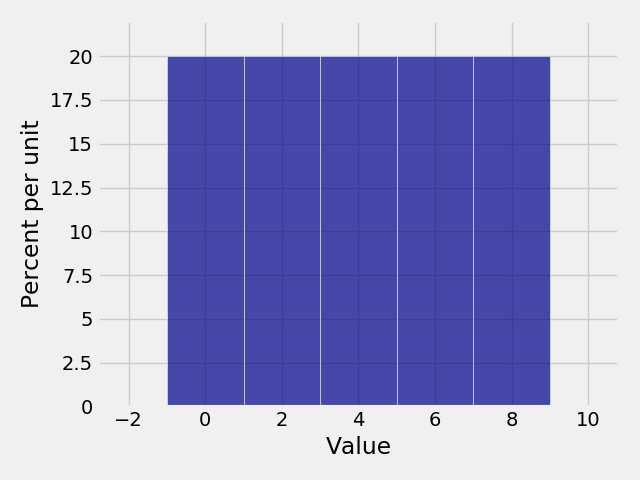
Events

Sometimes, we want to highlight an event or events in our histogram. To make an event a different color, we can use the optional parameter event=. An event must be a list or a list of lists.

In [27]: Plot(binomial, event=[1,3,5])

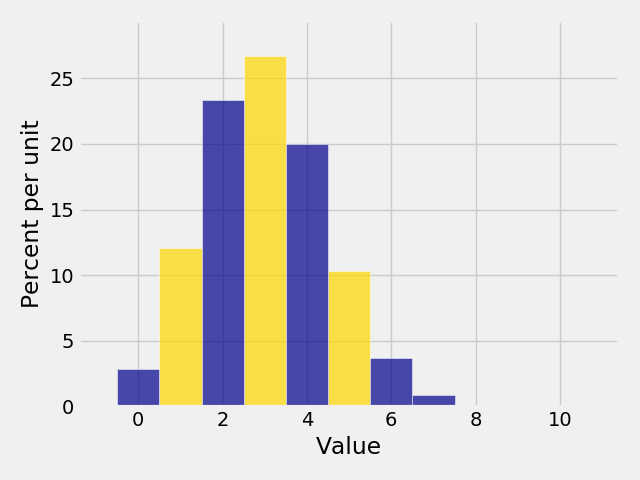
In [28]: Plot(binomial, event=np.arange(0,10,2))

If we use a list of lists for the event parameter, each event will be a different color.

In [29]: Plot(binomial, event=[[0],[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]])

Plotting multiple distributions

It is often useful to plot multiple histograms on top of each other. To plot multiple distributions on the same graph, use the Plots function. Plots takes in an even number of arguments, alternating between the label of the distribution and the distribution table itself.

In [30]: Plots("Distribution 1", dist1, "Distribution 2", dist2)

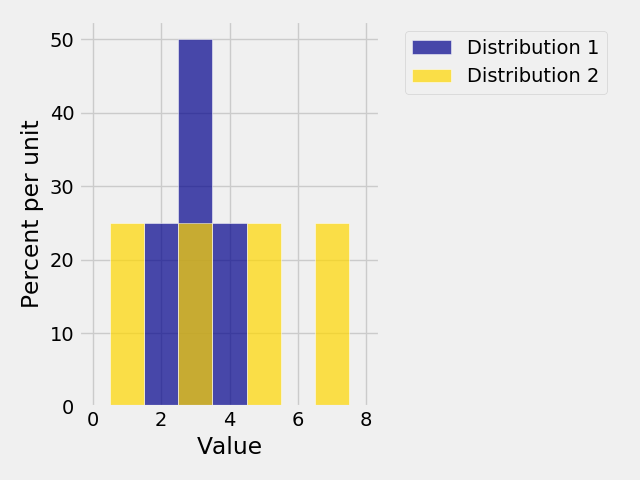
In [31]: binomial2 = Table().values(np.arange(11)).probability_function(lambda x: comb(10,x) * 0.5**10)

In [32]: Plots("Bin(n=10,p=0.3)", binomial, "Bin(n=10,p=0.5)", binomial2)

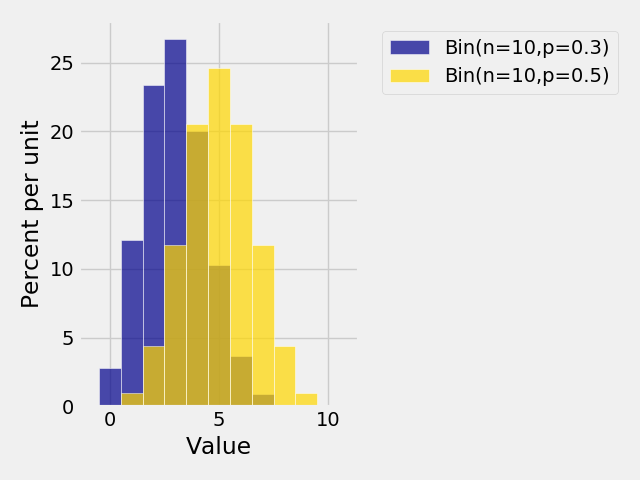
Try to avoid plotting too many distributions together because the graph starts to become unreadable

In [33]: Plots("dist1", dist1, "dist2", dist2, "Bin1", binomial, "Bin2", binomial2)

Empirical Distributions

Whenever we simulate an event, we often end up with an array of results. We can construct an empirical distribution of the results by grouping of the possible values and assigning the frequencies as probabilities. Simply call emp_dist

In [34]: x = make_array(1,1,1,1,1,2,3,3,3,4)

In [35]: emp_dist(x)
Out[35]: 
Value | Proportion
1     | 0.5
2     | 0.1
3     | 0.3
4     | 0.1

In [36]: values = make_array()

In [37]: for i in range(10000):
   ....:     num = np.random.randint(10) + np.random.randint(10) + np.random.randint(10) + np.random.randint(10)
   ....:     values = np.append(values, num)
   ....: 

In [38]: Plot(emp_dist(values))

Utilities

There are also utility functions for finding the expected value (ev()), variance (var()), or standard deviation (sd()) of a distribution.

In [39]: print(dist1.ev())
3.0

In [40]: print(dist1.sd())
0.7071067811865476

In [41]: print(binomial.ev())
3.000000000000001

In [42]: print(0.3 * 10)
3.0

In [43]: print(binomial.sd())
1.4491376746189442

In [44]: import math

In [45]: print(math.sqrt(10 * 0.3 * 0.7))
1.4491376746189437

In [46]: print(binomial.var())
2.100000000000001

In [47]: print(10 * 0.3 * 0.7)
2.0999999999999996