Independence¶

Jointly distributed random variables $X$ and $Y$ are independent if $$ P(X \in A, Y \in B) = P(X \in A)P(Y \in B) $$ for all intervals $A$ and $B$.

Let $X$ have density $f_X$, let $Y$ have density $f_Y$, and suppose $X$ and $Y$ are independent. Then if $f$ is the joint density of $X$ and $Y$,

\begin{align*} f(x, y)dxdy &\sim P(X \in dx, Y \in dy) \\ &= P(X \in dx)P(Y \in dy) ~~~~~ \text{(independence)} \\ &= f_X(x)dx f_Y(y)dy \\ &= f_X(x)f_Y(y)dxdy \end{align*}

Thus if $X$ and $Y$ are independent then their joint density is given by

$$ f(x, y) = f_X(x)f_Y(y) $$

This is the product rule for densities: the joint density of two independent random variables is the product of their densities.

Independent Standard Normal Random Variables¶

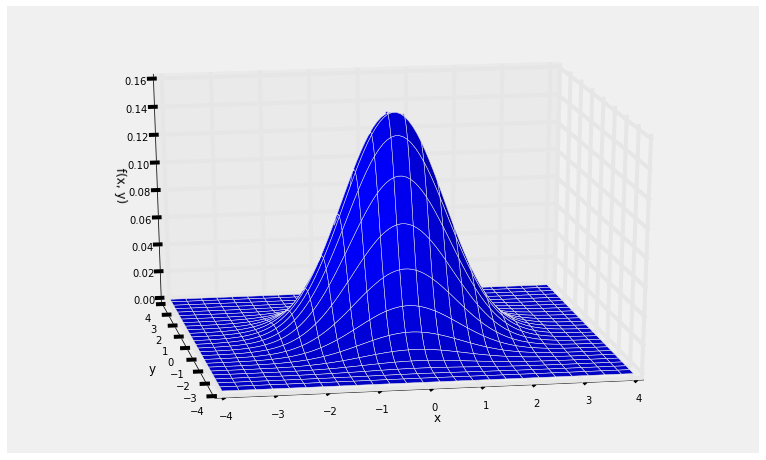
Suppose $X$ and $Y$ are i.i.d. standard normal random variables. Then their joint density is given by

$$ f(x, y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2} \cdot \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}y^2}, ~~~~ -\infty < x, y < \infty $$

Equivalently, $$ f(x, y) = \frac{1}{2\pi} e^{-\frac{1}{2}(x^2 + y^2)}, ~~~~ -\infty < x, y < \infty $$

Here is a graph of the joint density surface.

Notice the circular symmetry of the surface. This is because the formula for the joint density involves the pair $(x, y)$ through the expression $x^2 + y^2$ which is symmetric in $x$ and $y$.

Notice also that $P(X = Y) = 0$, as the probability is the volume over a line. This is true of all pairs of independent random variables with a joint density: $P(X = Y) = 0$. So for example $P(X > Y) = P(X \ge Y)$. You don't have to worry about whether or not to the inequality should be strict.

The Larger of Two Independent Exponential Random Variables¶

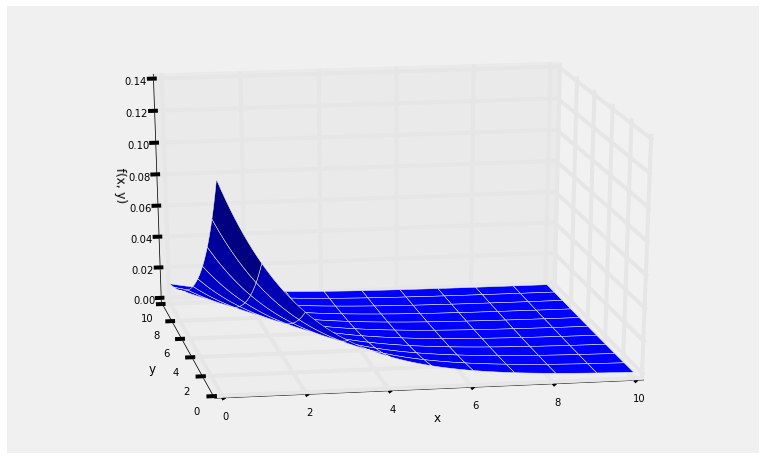
Let $X$ and $Y$ be independent random variables. Suppose $X$ has the exponential $(\lambda)$ distribution and $Y$ has the exponential $(\mu)$ distribution. The goal of this example is to find $P(Y > X)$.

By the product rule, the joint density of $X$ and $Y$ is given by

$$ f(x, y) ~ = ~ \lambda e^{-\lambda x} \mu e^{-\mu y}, ~~~~ x > 0, ~ y > 0 $$

The graph below shows the joint density surface in the case $\lambda = 0.5$ and $\mu = 0.25$, so that $E(X) = 2$ and $E(Y) = 4$.

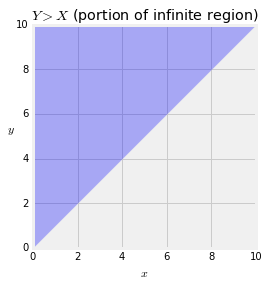
To find $P(Y > X)$ we must integrate the joint density over the upper triangle of the first quadrant, a portion of which is shown below.

The probability is therefore $$ P(Y > X) ~ = ~ \int_0^\infty \int_x^\infty \lambda e^{-\lambda x} \mu e^{-\mu y} dy dx $$

We can do this double integral without much calculus, just by using probability facts.

\begin{align*} P(Y > X) &= \int_0^\infty \int_x^\infty \lambda e^{-\lambda x} \mu e^{-\mu y} dy dx \\ \\ &= \int_0^\infty \lambda e^{-\lambda x} \big{(} \int_x^\infty \mu e^{-\mu y} dy\big{)} dx \\ \\ &= \int_0^\infty \lambda e^{-\lambda x} e^{-\mu x} dx ~~~~~~ \text{(survival function of } Y\text{, evaluated at } x \text{)} \\ \\ &= \frac{\lambda}{\lambda + \mu} \int_0^\infty (\lambda + \mu) e^{-(\lambda + \mu)x} dx \\ \\ &= \frac{\lambda}{\lambda + \mu} ~~~~~~~ \text{(total integral of exponential } (\lambda + \mu) \text{ density is 1)} \end{align*}

Thus $$ P(Y > X) ~ = ~ \frac{\lambda}{\lambda + \mu} $$ Analogously, $$ P(X > Y) ~ = ~ \frac{\mu}{\lambda + \mu} $$

Notice that the two chances are proportional to the parameters. This is consistent with intuition if you think of $X$ and $Y$ as two lifetimes. If $\lambda$ is large, the corresponding lifetime $X$ is likely to be short, and therefore $Y$ is likely to be larger than $X$ as the formula implies.

If $\lambda = \mu$ then $P(Y > X) = 1/2$ which you can see by symmetry since $P(X = Y) = 0$.

If we had attempted the double integral in the other order – first $x$, then $y$ – we would have had to do more work. The integral is

$$ \int_0^\infty \int_0^y \lambda e^{-\lambda x} \mu e^{-\mu y} dx dy $$

Let's do it in SymPy to check that the answer comes out the same.

Keep in mind that SymPy doesn't like to display negative exponents, so some functions appear in a different form compared to the way we usually write them.

That looks strange but it is equal to

$$ 1 - \frac{\mu}{\lambda + \mu} ~ = ~ \frac{\lambda}{\lambda + \mu} $$

which is the same as the answer we got earlier.