Examples
Examples¶
Here are two examples that make use of much of what you have learned in the last couple of chapters.
A Diffusion Model by Ehrenfest¶
Paul Ehrenfest proposed a number of models for the diffusion of gas particles, one of which we will study here.
The model says that there are two containers containing a total of $N$ particles. At each instant, a container is selected at random and a particle is selected at random independently of the container. Then the selected particle is placed in the selected container; if it was already in that container, it stays there.
Let $X_n$ be the number of particles in Container 1 at time $n$. Then $X_0, X_1, \ldots$ is a Markov chain with transition probabilities given by:
\begin{equation} P(i, j) = \begin{cases} \frac{N-i}{2N} & \text{if } j = i+1 \\ \frac{1}{2} & \text{if } j = i \\ \frac{i}{2N} & \text{if } j = i-1 \\ 0 & \text{otherwise} \end{cases} \end{equation}The chain is clearly irreducible. It is aperiodic because $P(i, i) > 0$.
Question. What is the stationary distribution of the chain?
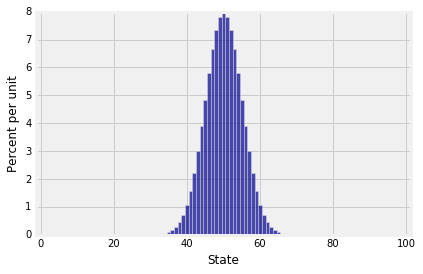
Answer. We have computers. So let's first find the stationary distribution for $N=100$ particles, and then see if we can identify it for general $N$.
N = 100
s = np.arange(N+1)
def trans_probs(i, j):
if j == i:
return 1/2
if j == i+1:
return (N-i)/(2*N)
elif j == i-1:
return i/(2*N)
else:
return 0
tbl = Table().states(s).transition_function(trans_probs)
ehrenfest = tbl.toMarkovChain()
Plot(ehrenfest.steady_state(), edges=True)
That looks suspiciously like the binomial (100, 1/2) distribution. In fact it is the binomial (100, 1/2) distribution. Since you've guessed it, all you have to do is plug it into the balance equations and check that they work out.
The balance equations are:
\begin{align*} \pi(0) &= \frac{1}{2}\pi(0) + \frac{1}{2N}\pi(1) \\ \pi(j) &= \frac{N-(j-1)}{2N}\pi(j-1) + \frac{1}{2}\pi(j) + \frac{j+1}{2N}\pi(j+1), ~~~ 1 \le j \le N-1 \\ \pi(N) &= \frac{1}{2N}\pi(N-1) + \frac{1}{2}\pi(N) \end{align*}You have already guessed the solution by looking at the answer calculated for $N=100$. But if you want to start from scratch, you'll have to simplify the balance equations and try to write all the elements of $\pi$ in terms of $\pi(0)$. You will get:
\begin{align*} \pi(1) &= N\pi(0) \\ \\ \pi(2) &= \frac{N(N-1)}{2} \pi0 = \binom{N}{2} \pi(0) \end{align*}and so on by induction:
$$ \pi(j) = \binom{N}{j} \pi(0) $$In other words, the stationary distribution is proportional to the binomial coefficients. So $\pi(0) = 1/2^n$ to make all the elements sum to 1, and the distribution is binomial $(N, 1/2)$.
Expected Reward¶
Suppose I run the lazy reflecting random walk from the previous section for a long time. As a reminder, here is its stationary distribution.
stationary = refl_walk.steady_state()
stationary
Question 1. Suppose that every time the chain is in state 4, I win $\$4$; every time it's in state 5, I win $\$5$; otherwise I win nothing. What is my expected long run average reward?
Answer 1. In the long run, the chain is in steady state. So I expect that on 62.5% of the moves I will win nothing; on 25% of the moves I will win $\$4$; and on 12.5% of the moves I will win $\$5$. My expected long run average reward per move is $\$1.625$.
0*0.625 + 4*0.25 + 5*.125
Question 2. Suppose that every time the chain is in state $i$, I toss $i$ coins and record the number of heads. In the long run, how many heads do I expect to get on average per move?
Answer 2. Each time the chain is in state $i$, I expect to get $i/2$ heads. When the chain is in steady state, the expected number of coins I toss at any given move is 3. So, by iterated expectations, the long run average number of heads I expect to get is 1.5.
stationary.expected_value()/2
If that seems artificial, consider this: Suppose I play the game above, and on every move I tell you the number of heads that I get but I don't tell you which state the chain is in. I hide the underlying Markov Chain. If you try to recreate the sequence of steps that the Markov Chain took, you are working with a Hidden Markov Model. These are much used in pattern recognition, bioinformatics, and other fields.