Monotone Functions
The method we have developed for finding the density of a linear function of a random variable can be extended to non-linear functions. We will start with a setting in which you have seen that applying non-linear functions to a random variable can have useful results.
Simulation via the CDF
In exercises, you have seen by simulation that you can generate a value of a random variable with a specified distribution by using the cdf of the distribution and a uniform (0, 1) random number. We will now establish the theory that underlies what you discovered by computation.
Let F be a differentiable, strictly increasing cdf on the real number line. The differentiability assumption allows you to find the corresponding density by differentiating.
Our goal is to generate a value of a random variable that has F as its cdf. The statement below describes the process that you came up with in exercises. Note that because F is continuous and strictly increasing, it has an inverse function.
Let U have the uniform (0, 1) distribution. Define a random variable X by the formula X=F−1(U), and let FX be the cdf of X. We will show that FX=F and thus that X has the desired distribution.
To prove the result, remember that the cdf FU of U is given by FU(u)=u for 0<u<1. Let x be any number. Our goal is to show that FX(x)=F(x).
FX(x) = P(X≤x)= P(F−1(U)≤x)= P(U≤F(x)) because F is increasing= FU(F(x))= F(x)Change of Variable Formula for Density: Increasing Function
The function F−1 is differentiable and increasing. We will now develop a general method for finding the density of such a function applied to any random variable that has a density.
Let X have density fX. Let g be a smooth (that is, differentiable) increasing function, and let Y=g(X). Examples of such functions g are:
- g(x)=ax+b for some a>0. This case was covered in the previous section.
- g(x)=ex
- g(x)=√x on positive values of x
To develop a formula for the density of Y in terms of fX and g, we will start with the cdf as we did above.
Let g be smooth and increasing, and let Y=g(X). We want a formula for fY. We will start by finding a formula for the cdf FY of Y in terms of g and the cdf FX of X.
FY(y) = P(Y≤y)= P(g(X)≤y)= P(X≤g−1(y)) because g is increasing= FX(g−1(y))Now we can differentiate to find the density of Y. By the chain rule and the fact that the derivative of an inverse is the reciprocal of the derivative,
fY(y) = fX(g−1(y))ddyg−1(y)= fX(x)1g′(x) at x=g−1(y)The Formula
Let g be a differentiable, increasing function. The density of Y=g(X) is given by
fY(y) = fX(x)g′(x) at x=g−1(y)Understanding the Formula
To see what is going on in the calculation, we will follow the same process as we used for linear functions in an earlier section.
- For Y to be y, X has to be g−1(y).
- Since g need not be linear, the tranformation by g won’t necessarily stretch the horizontal axis by a constant factor. Instead, the factor has different values at each x. If g′ denotes the derivative of g, then the stretch factor at x is g′(x), the rate of change of g at x. To make the total area under the density equal to 1, we have to compensate by dividing by g′(x). This is valid because g is increasing and hence g′ is positive.
This gives us an intuitive justification for the formula.
Applying the Formula
Let X have the exponential (1/2) density and let Y=√X. We can take the square root because X is a positive random variable.
Let’s find the density of Y by applying the formula we have derived above. We will organize our calculation in four preliminary steps, and then plug into the formula.
- The density of the original random variable: The density of X is fX(x)=(1/2)e−(1/2)x for x>0.
- The function being applied to the original random variable: Take g(x)=√x. Then g is increasing and its possible values are (0,∞).
- The inverse function: Let y=g(x)=√x. We will now write x in terms of y, to get x=y2.
- The derviative: The derivative of g is given by g′(x)=1/(2√x).
We are ready to plug this into our formula. Keep in mind that the possible values of Y are (0,∞). For y>0 the formula says
fY(y) = fX(x)g′(x) at x=g−1(y)So for y>0,
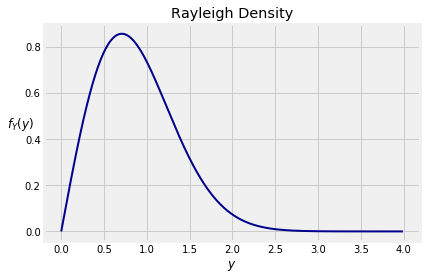
fY(y) = (1/2)e−12x1/(2√x) at x=y2= √xe−12x at x=y2= √y2e−12y2= ye−12y2This is called the Rayleigh density. Its graph is shown below.
Change of Variable Formula for Density: Monotone Function
Let g be smooth and monotone (that is, either increasing or decreasing). The density of Y=g(X) is given by
fY(y) = fX(x)|g′(x)| at x=g−1(y)We have proved the result for increasing g. When g is decreasing, the proof is analogous to proof in the linear case and accounts for g′ being negative. We won’t take the time to write it out.
Reciprocal of a Uniform Variable
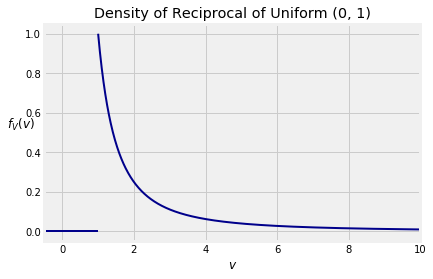
Let U be uniform on (0,1) and let V=1/U. The distribution of V is called the inverse uniform but the word “inverse” is confusing in the context of change of variable. So we will simply call V the reciprocal of U.
To find the density of V, start by noticing that the possible values of V are in (1,∞) as the possible values of U are in (0,1).
The components of the change of variable formula for densities:
- The original density: fU(u)=1 for 0<u<1.
- The function: Define g(u)=1/u.
- The inverse function: Let v=g(u)=1/u. Then u=g−1(v)=1/v.
- The derivative: Then g′(u)=−u−2.
By the formula, for v>1 we have
fV(v) = fU(u)|g′(u)| at u=g−1(v)That is, for v>1,
fV(v) = 1⋅u2 at u=1/vSo
fV(v) = 1v2, v>1You should check that fV is indeed a density, that is, it integrates to 1. You should also check that the expectation of V is infinite.
The density fV belongs to the Pareto family of densities, much used in economics.