10.4. Examples

Here are two examples to illustrate how to find the stationary distribution and how to use it.

10.4.1. A Diffusion Model by Ehrenfest

Paul Ehrenfest proposed a number of models for the diffusion of gas particles, one of which we will study here.

The model says that there are two containers containing a total of \(N\) particles. At each instant, a container is selected at random and a particle is selected at random independently of the container. Then the selected particle is placed in the selected container; if it was already in that container, it stays there.

Let \(X_n\) be the number of particles in Container 1 at time \(n\). Then \(X_0, X_1, \ldots\) is a Markov chain with transition probabilities given by:

\[\begin{split} \begin{equation} P(i, j) = \begin{cases} \frac{N-i}{2N} & \text{if } j = i+1 \\ \frac{1}{2} & \text{if } j = i \\ \frac{i}{2N} & \text{if } j = i-1 \\ 0 & \text{otherwise} \end{cases} \end{equation} \end{split}\]

The chain is clearly irreducible. It is aperiodic because \(P(i, i) > 0\).

Question: What is the stationary distribution of the chain?

Answer: We have computers. So let’s first find the stationary distribution for \(N=100\) particles, and then see if we can identify it for general \(N\).

N = 100

states = np.arange(N+1)

def transition_probs(i, j):
    if j == i:
        return 1/2
    elif j == i+1:
        return (N-i)/(2*N)
    elif j == i-1:
        return i/(2*N)
    else:
        return 0

ehrenfest = MarkovChain.from_transition_function(states, transition_probs)
Plot(ehrenfest.steady_state(), edges=True)

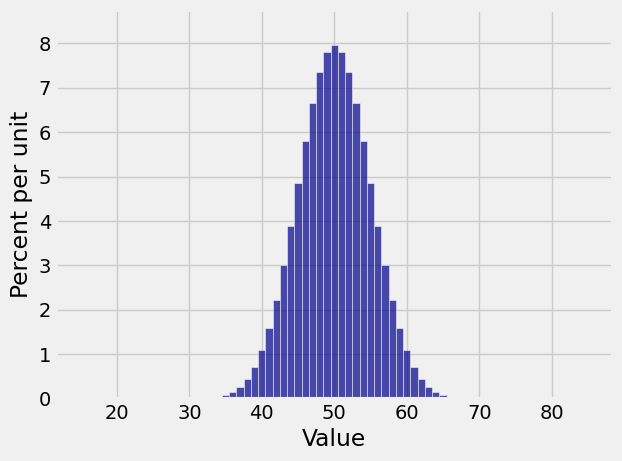
That looks suspiciously like the binomial (100, 1/2) distribution. In fact it is the binomial (100, 1/2) distribution. Let’s solve the balance equations to prove this.

The balance equations are:

\[\begin{split} \begin{align*} \pi(0) &= \frac{1}{2}\pi(0) + \frac{1}{2N}\pi(1) \\ \pi(j) &= \frac{N-(j-1)}{2N}\pi(j-1) + \frac{1}{2}\pi(j) + \frac{j+1}{2N}\pi(j+1), ~~~ 1 \le j \le N-1 \\ \pi(N) &= \frac{1}{2N}\pi(N-1) + \frac{1}{2}\pi(N) \end{align*} \end{split}\]

Now rewrite each equation to express all the elements of \(\pi\) in terms of \(\pi(0)\). You will get:

\[\begin{split} \begin{align*} \pi(1) &= N\pi(0) \\ \\ \pi(2) &= \frac{N(N-1)}{2} \pi(0) = \binom{N}{2} \pi(0) \end{align*} \end{split}\]

and so on by induction:

\[ \pi(j) = \binom{N}{j} \pi(0), ~~~~~~~~ 1 \le j \le N \]

This is true for \(j = 0\) as well, since \(\binom{N}{0} = 1\).

Therefore the stationary distribution is

\[ \pi ~ = ~ \big{[} \binom{N}{0}\pi(0), \binom{N}{1}\pi(0), \binom{N}{2}\pi(0), \ldots, \binom{N}{N}\pi(0) \big{]} \]

In other words, the stationary distribution is proportional to the binomial coefficients. Now

\[ \sum_{j=0}^N \binom{N}{j} ~ = ~ (1 + 1)^N = 2^N \]

So \(\pi(0) = 1/2^N\) and the stationary distribution is binomial \((N, 1/2)\).

10.4.2. Expected Reward

Suppose I run the sticky reflecting random walk from the previous section for a long time. As a reminder, here is its stationary distribution.

stationary = reflecting_walk.steady_state()
stationary

Value	Probability
1	0.125
2	0.25
3	0.25
4	0.25
5	0.125

Question 1: Suppose that every time the chain is in state 4, I win 4 dollars; every time it’s in state 5, I win 5 dollars; otherwise I win nothing. What is my expected long run average reward?

Answer 1: In the long run, the chain is in steady state. So I expect that on 62.5% of the moves I will win nothing; on 25% of the moves I will win 4 dollars; and on 12.5% of the moves I will win 5 dollars. My expected long run average reward per move is 1.65 dollars.

0*0.625 + 4*0.25 + 5*.125

1.625

Question 2: Suppose that every time the chain is in state \(i\), I toss \(i\) coins and record the number of heads. In the long run, how many heads do I expect to get on average per move?

Answer 2: Each time the chain is in state \(i\), I expect to get \(i/2\) heads. When the chain is in steady state, the expected number of coins I toss at any given move is 3. So, by iterated expectations, the long run average number of heads I expect to get is 1.5.

stationary.ev()/2

1.5000000000000022

If that seems artificial, consider this: Suppose I play the game above, and on every move I tell you the number of heads that I get but I don’t tell you which state the chain is in. I hide the underlying Markov Chain. If you try to recreate the sequence of steps that the Markov Chain took, you are working with a Hidden Markov Model. These are much used in pattern recognition, bioinformatics, and other fields.