14.4. SciPy and Normal Curves#
14.4.1. Plotting Normal Curves#
The prob140 function Plot_norm takes three arguments and displays the corresponding normal curve. The arguments are:
the interval over which to draw the curve, as a list or array with the two endpoints
the mean
the SD
Plot_norm([-4, 4], 0, 1)
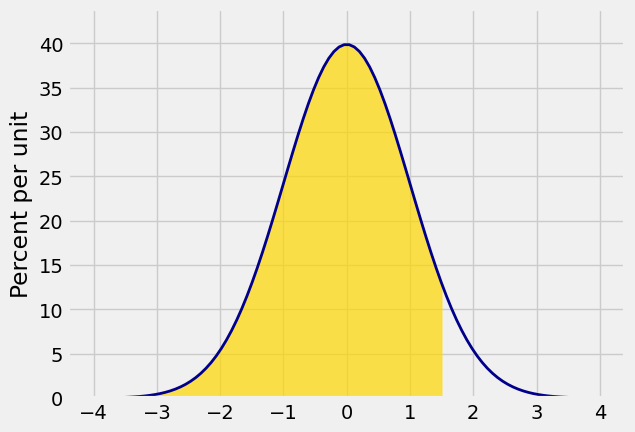
You can shade all the area to the left of a point right_end of the interval
Plot_norm([-4, 4], 0, 1, right_end=1.5)
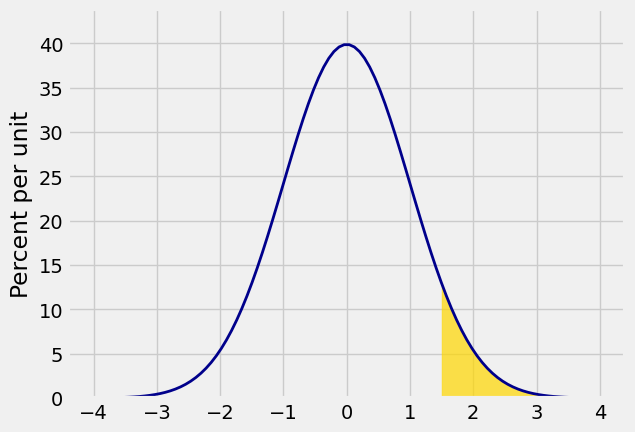
All the area to the right of a point:
Plot_norm([-4, 4], 0, 1, left_end=1.5)
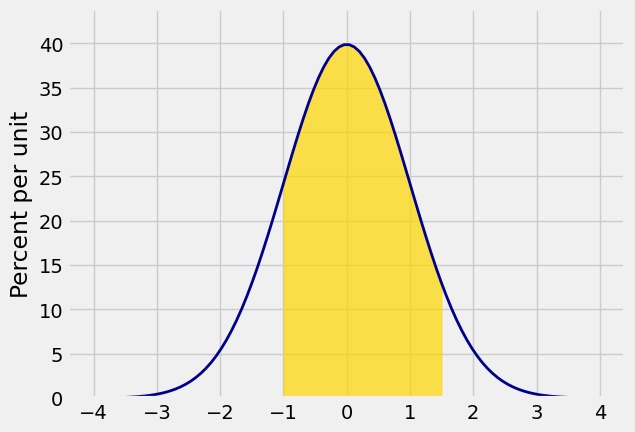
The area between two points:
Plot_norm([-4, 4], 0, 1, right_end=-1, left_end=1.5)
14.4.2.
All the areas displayed above can be expressed in terms of the standard normal cdf
Recall that the standard normal cdf
where
For each
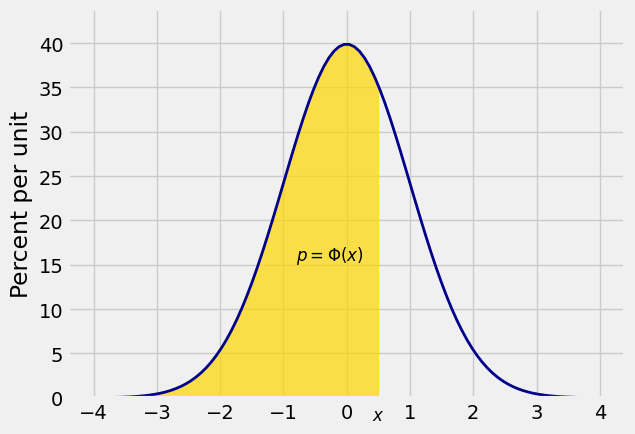
It will also be helpful to go the other way, and identify the
For each
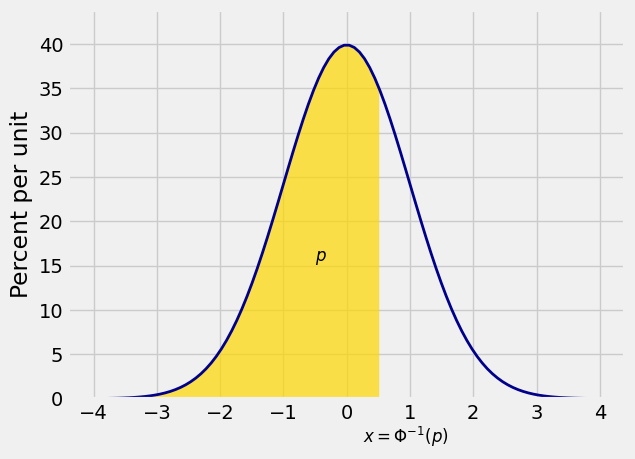
14.4.3. SciPy#
As we noted in the previous section, there is no closed form formula for
In SciPy the approximations are in the familiar stats module. For the standard normal cdf, use stats.norm.cdf just as you used stats.binom.cdf and so on. By default, stats.norm.cdf is based on the standard normal curve.
The area to the left of
stats.norm.cdf(1)
0.84134474606854293
The area between
stats.norm.cdf(1) - stats.norm.cdf(-1)
0.68268949213708585
In both examples above, we started with a point or points on the horizontal axis and used the cdf
For example, if you want stats.norm.ppf. The name comes from the expression “90% point” of the distribution, or equivalently, the 90th percentile.
stats.norm.ppf(0.9)
1.2815515655446004
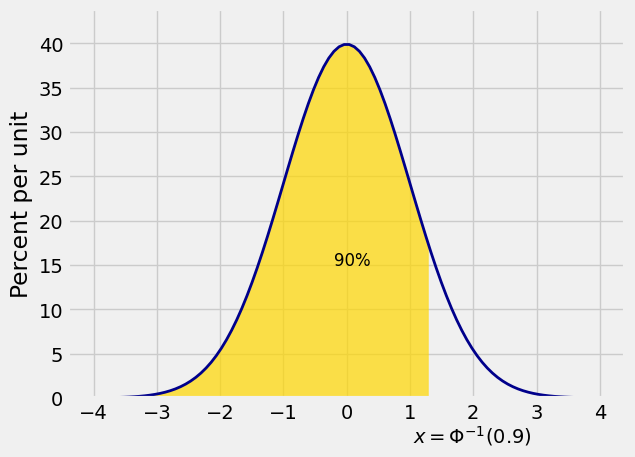
By the definition of an inverse, we should have
stats.norm.cdf(stats.norm.ppf(0.9))
0.89999999999999991
14.4.4. Example#
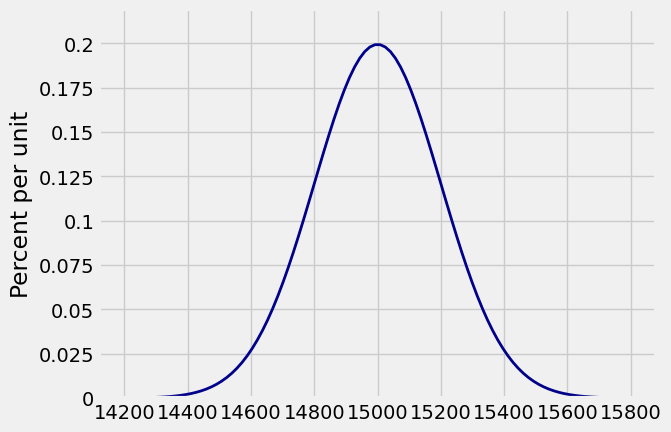
Suppose the weights of a sample of 100 people are i.i.d. with a mean of 150 pounds and an SD of 20 pounds. Then the total weight of the sampled people is roughly normal with mean
Who cares about the total weight of a random group of people? Ask those who construct stadiums, elevators, and airplanes.
# Approximate distribution of total weight
n = 100
mu = 150
sigma = 20
mean = n*mu
sd = (n**0.5)*sigma
plot_interval = make_array(mean-4*sd, mean+4*sd)
Plot_norm(plot_interval, mean, sd)
The chance that the total weight of the sampled people is less than 15,100 pounds is approximately the gold area below. The CLT allows us to use the normal curve as an approximation to the unknown exact distribution of the total weight.
Plot_norm(plot_interval, mean, sd, right_end=15100)
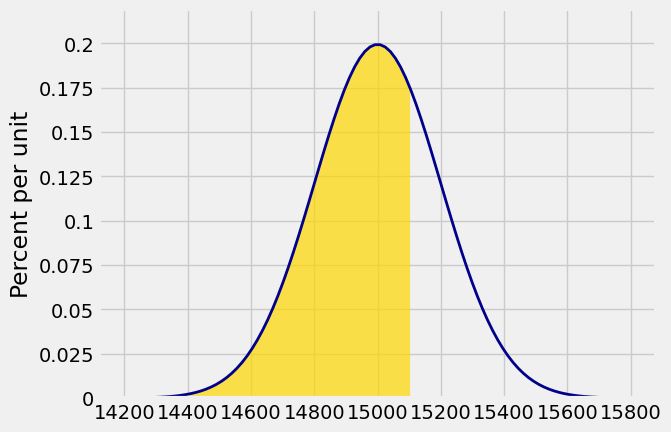
The function stats.norm.cdf takes the mean and SD as optional arguments. Remember that the names mean and sd were assigned in an earlier cell. Also remember that the answer below is not exact but an approximation based on the CLT.
stats.norm.cdf(15100, mean, sd)
0.69146246127401312
To find the approximate 90th percentile of the distribution of weights, you can use stats.norm.ppf with the mean and SD as arguments.
stats.norm.ppf(0.9, mean, sd)
15256.310313108919
The conclusion is
14.4.5. Using Standard Units#
While it convenient to be able to enter the mean and SD as arguments to stats.norm.cdf and stats.norm.ppf, the fundamental curve is the standard normal curve. All the others are obtained by linear transformations.
Therefore all the calculations above can be done in terms of the standard normal cdf by standardizing, and therefore all normal approximations can (and will) be written in terms of the standard normal cdf
For example, we can redo the two calculations above as follows.
To find the approximate chance that the total weight is less than 15100 pounds, first standardize 15100 and then use the standard normal cdf:
The calculation gives the same answer as before.
z = (15100 - mean)/sd
stats.norm.cdf(z)
0.69146246127401312
To find 90th percentile of the approximate distribution of the
z = stats.norm.ppf(0.9)
z
1.2815515655446004
Now convert the standard units back to pounds. The 90th percentile of the distribution of
x = z*sd + mean
x
15256.310313108919

